If you are not interested in the theoretical background, just jump down to the summary.
See also:
Troggle report: UTM/G&K entrance data
Troggle report: entrances
GPS and coordinate systems
Basic Coordinate Systems.
Geographical fixed points on Loser
The Austrian Kataster areas
SD 10 Handbook: Vergleich der ÖK 50 mit der neuen ÖK 50-UTM
Location fixing: How to obtain a fixed point for a cave survey
When dealing with geographical data like cave locations, you will inevitably run into a whole zoo of coordinate systems with names like WGS84, UTM, BMN and so on. While a thorough introduction is probably more appropriate for a full course in geodesy, I'll try to summarise the most important bits as far as they are relevant to us and as far as I understand them myself.

In a first approximation the earth is a sphere. And unfortunately there are some mathematical proofs showing that it's not possible to project the surface of a sphere onto a 2D plane or map without distortions. People have still tried hard and come up with a particular projection called the Transversal Mercator projection, which has beneficial properties summarised as "locally there are almost no distortions".
The non-transversal, standard Mercator projection essentially takes a cylinder aligned with the rotational axis of the earth from north to south and wraps the cylinder around the equator of the earth. Next all the important landmarks are projected onto the cylinder by casting rays from the centre of the earth through its surface and onto the cylinder. Once everything is mapped, the cylinder is cut open and unwrapped onto a flat table and ready is your map. This map will be very accurate and have very little distortions around the equator, but the closer you get to the poles the more distortions will become noticeable. In particular think of where the north and south poles will be projected to.
The Transversal Mercator projection is very similar to the above, but instead of aligning the cylinder with a north-south axis and intersecting earth along the equator, it is tilted sideways, aligned with an east-west axis and intersects earth in a circle for example along the 0-meridian through Greenwich, through the poles, and somewhere through the Pacific. The rest is done as before and once you cut the cylinder open and unwrap it, you'll get an accurate map with little distortions exactly around the line of intersection, which is called the "central meridian" of this particular Transversal Mercator projection. Of course America and China would be heavily distorted with the above choice of central meridian. So instead of doing just one of these Transversal Mercator projections globally, the earth is divided into e.g. 60 zones and a different cylinder with a different central meridian is selected for each zone. One particular definition of such zones has been internationally standardised as Universal Transversal Mercator coordinates, but for the entertainment of the local geodesists, different local coordinate systems and "zones" have been defined for many countries. In Germany this is called "Gauss-Krüger (GK)", in Austria there is a definition called "Bundesmeldenetz (BMN)", and in the UK it is the "British National Grid (BNG)".
One more thing. Once you have your unwrapped cylinder you'll have to define coordinates on this cylinder surface, your map. These are usually metric coordinates, i.e. they specify how many metres you have to walk north and east on the cylinder surface starting from a given origin. And typically one starts the "easting" at for example the western boundary of a zone and the "northing" at the equator. For a national Austrian grid, it doesn't make sense to start at the equator and therefore some "false easting" and "false northing" have been defined by omitting some of the leading digits. This saves repeatedly typing all the same prefixes over and over again.
Unfortunately the earth is not a sphere. A slightly more accurate representation would be an ellipsoid, that is wider around the equator and flatter at the poles. This has long been known and the Transversal Mercator projection has been adapted to an ellipsoidal shape, so that it has even less distortions. And of course, many clever people have come up with many clever approximations of the ellipsoid. For example, the British National Grid uses an ellipsoid defined by someone called Airy in 1830, and Bessel has come up with a different ellipsoid in 1841. These were computed by making accurate astronomical observations at different places within Europe. In contrast, the more modern WGS84 ellipsoid has been defined by satellite observations in more recent times.
The different ellipsoids not only vary in their major and minor axes, but also the centre of the ellipsoids can be offset or the whole ellipsoid can be rotated by a bit. So these offset and rotation parameters have to be specified as well, and getting the ellipsoid parameters wrong would typically result in coordinates that are around 500m off, which is unacceptable for locating a cave entrance on the plateau. So we can't just ignore the ellipsoids but have to get their definitions right.

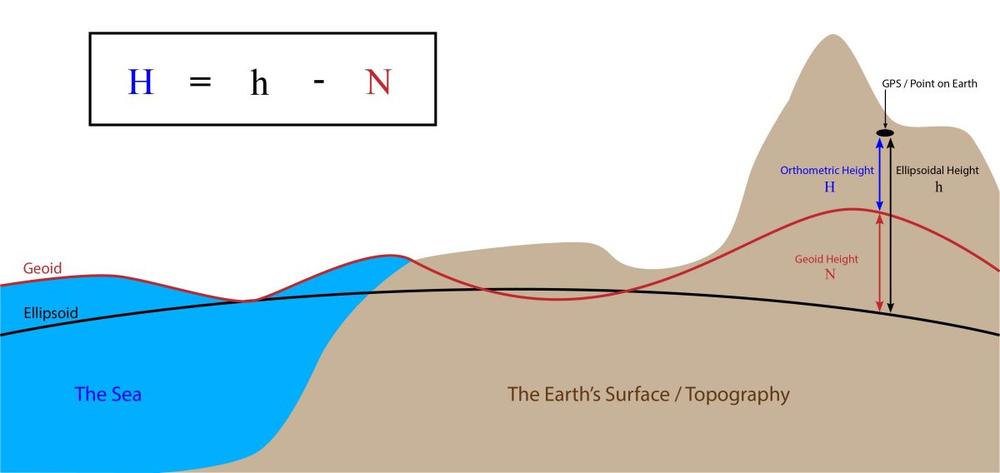
Unfortunately the earth is not an ellipsoid either, but rather something like a potato. This is not so important for defining east and north coordinates, but it is very important for defining altitudes. While one sensible definition of altitudes would simply be the "height above ellipsoid", it actually makes quite a bit of sense to rethink this definition and come up with something different, called geoids (not to be confused with ellipsoids!).
Traditionally height was defined by "mean sea level", and in Austria they use something called "Gebrauchshöhen Adria", which is meant to be the height above the Adriatic sea. Unfortunately you can only measure the mean sea level along the coast and it becomes a bit more difficult in the mountains. So starting from a single point defined as the mean sea level in Trieste in 1875 or so, the Austrians started to triangulate a grid of survey stations across all of their empire. According to this triangulation they ended up with several reference heights of certain peaks and so on, which is not necessarily the real height above Adria anymore but includes some errors. Still, these reference heights make up the "Gebrauchshöhe Adria", which literally means something like "Used Height Adria".
As clinos are affected by gravity, so are the Austrian triangulations, and it turns out that the mass of the continental plates does indeed affect gravity. So if you simply approximate the mean sea level by a "simple" ellipsoid such as the "height above ellipsoid" does, then you end up with a completely different set of altitudes compared to the triangulation results. It turns out that relative to the ellipsoid the "mean sea level" at some point in the alps would be about 40m above the mean sea level at some point along the coast, just because the heavy continental crust would attract more water. The "Gebrauchshöhen Adria" have been defined with exactly this mass anomaly, and that's what the Austrians use to this date.
Nowadays geodesists have come up with something called geoids. These geoids define the shape of equipotential surfaces, i.e. the shape of the surfaces along which a reference body would have the same potential energy in the gravity field of the earth. So in a sense, the Austrians defined a small portion of a geoid by measuring the gravity field and defining their "Gebrauchshöhen Adria" accordingly. In the meantime, some other geoids have been defined and refined using satellite measurements and so on. There are plenty of them available as huge "geoid height above ellipsoid"-tables in some massive files (well, 4MB for the old, simple geoid models, 200MB for more modern and accurate ones).
Most modern GPS receivers, at least most Garmin ones, will nowadays compute a "height above sea level", and not a "height above ellipsoid". Unfortunately at least Garmin devices do not allow to change this, and the bad news is that in fact no one outside the Garmin Corporation really seems to know, how they managed to approximate the geoid in their tiny little units with not very much memory and computation power. But the good news is that the differences between various geoids are usually in the range of 25cm, and the Austrian "Gebrauchshöhen Adria" make no difference there. In fact, as the Bessel ellipsoid has been designed within Europe and adapted to the shape of the alps, even the differences between the Bessel ellipsoid and the "Gebrauchshöhen Adria" are below 3.5m for most parts of Austria and about 40cm on the Schwarzmooskogel.
Luckily all of the above is so horribly complicated, that people have long come up with computer programs for converting these coordinate systems back and forth. You just have to find an appropriate suite of software and learn how to use it. And particularly the using part can still be quite complicated. For the reasons detailed in the "Geoids" section above, I'd recommend converting only the horizontal coordinates and keeping the altitude measurements from the GPS.
I personally get along very well with Proj4, which is open source and free and all that. [We use survex for all our cordinate conversions these days - which uses proj4 internally - 2023].
Proj4 should also be packaged with all major Linux distributions and installed on the expo computer. Unfortunately the current versions do not deal very well with vertical datums (i.e. geoids), but we can ignore the geoids anyway. To invoke it, you have to type in something like
cs2cs +from [+some +magic +parameters] \
+to [+some +more +magic +parameters]
Then you type in the coordinates in the source format and you'll get coordinates in the destination system, sometimes with x and y swapped back and forth. The following table is intended to help you choose the right magic parameters for your coordinate system:
Latitude-Longitude in WGS84 datum with heights above WGS84 ellipsoid:
+proj=latlon +ellps=WGS84 +datum=WGS84 |
Latitude-Longitude in WGS84 datum with heights above EGM96 geoid[1]:
+proj=latlon +ellps=WGS84 +datum=WGS84 +geoidgrids=egm96_15.gtx |
UTM coordinates in WGS84 datum with heights above EGM96 geoid[1]:
+proj=utm +zone=33 +ellps=WGS84 +datum=WGS84 \ +geoidgrids=egm96_15.gtx |
Austrian coordinates for our Loser data set[2]:
+proj=tmerc +lat_0=0 +lon_0=13d20 +k=1 +x_0=0 +y_0=-5200000 \ +ellps=bessel +towgs84=577.326,90.129,463.919,5.137,1.474,5.297,2.4232 |
[1] Starting from version 4.8, the cs2cs program should have rudimentary support for vertical datums. You might have to separately install the file egm96_15.gtx, though. While this file strictly speaking only defines the EGM96 geoid, it can serve as a good approximation to most other geoids, including the one used by Garmin GPS receivers and the "Gebrauchshöhe Adria"
[2] There are a few different versions of the "+towgs84" part of the Austrian coordinate system, which specifies the offset and rotation of the used Bessel ellipsoid with respect to the WGS84 ellipsoid. According to an old table found on this expo website, it should read "575,93,466,5.1,5.1,5.2,2.5", which is clearly a mistyped version of the more commonly found definition "575,93,466,5.1,1.6,5.2,2.5". Both of these seem slightly less accurate than the "577.326,90.129,463.919,5.137,1.474,5.297,2.4232" proposed by various other sources, but in the end it will only make a difference of about a metre or so.
[These are Olaf's view in 2012. This is no longer what we use! Today we use WGS84 latitude and logitude just as it appears on your phone or GPS. (Note added May 2021)]
For all practical purposes [in 2012] I'd say, set your GPS receiver to UTM coordinates, WGS84 ellipsoid, WGS84 datum. [No: today in the 2020s set your phone to lat/long WGS84, digital degreees.]It will usually spit out rather unspecific "heights above sea level", which are within about 25cm of the heights in our data set. To convert the horizontal coordinates from UTM zone 33 to our data set coordinates, use:
cs2cs +from +proj=utm +zone=33 +ellps=WGS84 +datum=WGS84 \ +to +proj=tmerc +lat_0=0 +lon_0=13d20 +k=1 \ +x_0=0 +y_0=-5200000 +ellps=bessel \ +towgs84=577.326,90.129,463.919,5.137,1.474,5.297,2.4232
As an exercise you can try to convert the following between latitude-longitude, UTM and data set coordinates:
| Point | lat-long WGS84 | UTM WGS84 | data set |
|---|---|---|---|
| 161g | 13d49'35.982"E 47d41'1.807"N | 411941 5281827 | 37095.76 82912.23 |
| 204a | 13.82146667 47.69093333 | 411563 5282622 | 36700.78 83698.97 |
| 2001-06 | 13.81911639 47.67609556 | 411362 5280976 | 36534.63 82048.14 |
| 2011-01 | 13.82701861 47.69979611 | 411995 5283601 | 37111.31 84686.99 |
Olaf Kähler, September 2012
Return to GPS and coordinate systems.