CUCC Expo Surveying Handbook - LRUDs
Enhanced LRUD Recording
Andy Atkinson
A number of survey software packages now let you
include LRUD (Left Right Up Down) passage dimensions in some form
or other and will produce a plot using this information. All of
these, with the exception of Toporobot, are simplistic in their
approach, and if you have seen the output you will recognise the
rather odd-looking characteristic shapes that occur. There are
good reasons why this is so. The conventions that surveyors use
when recording the data, such as 'in the direction of the survey',
and 'across the passage' are not very easily defined in computing
terms. Also the fact that LRUDs are typically taken at stations,
and stations are often at junctions causes problems as junctions
tend to be atypical, rather than typical, of the passage. There
are a whole host of other things like what to do when a value
is not given, a question mark is entered, and at the ends of passages.
If zero is assumed at an omitted reading then a pinch-point occurs
in the walls at that station - not really the desired effect.
We have been examining the details of this process
with a view to implementing something in Survex, and generationg
a proper 3D model of the complex Kaninchenhohle. It quickly became
clear that as well as the programming difficulties there were
significant problems in terms of the data that was actually collected.
Obviously a set of 4 numbers conveys much less information than
a sketch. Unfortunately a sketch is inherently 2-dimensional,
and thus is not very helpful when trying to construct a 3D model.
So the question becomes - what is the least information that needs
to be recorded in order to construct a useful 3D model? Obviously
the answer depends on what you want to use the finished model
for, and the usual constraints on surveying manpower, time &
conditions.
Andy Atkinson took a look at the specific area
of improving the information contained in the LRUD data without
dramatically increasing the time it took to record, or the complexity
beyond the point which surveyors would stand (where relatively
inexperienced Cambridge Cavers in Austria's horrible caves have
a particularly low tolerance of such things). Obviously improvements
of this nature are no use if surveyors think they are too much
extra work. Here he presents his second iteration of the idea
for comment.
The computing aspects of LRUD interpretation and
the broader issues of wall modelling need articles of their own
to explore. These will be in future issues.
The suggested format is an extension of the now standard
LRUD, with a 5th column -'E' for Extension - which is used in
some cases. One obvious improvement is a notation for allowing
more than one value to be given in the same direction. This particularly
useful in traversable rift where you really want to indicate the
distance to both the actual and apparent floors, or sometimes
in a wide bedding where only the centre part is person-sized.
There are many possibly notations, all prone to confusion, or
not completely general.
- Two values separated by a slash is obvious except
that many people (CUCC included) use slash instead of the decimal
point, so that would be confusing.
- A secondary reading below the first may use an
extra line or be cramped, and which is which?.
- A comma-separated pair is plausible, but the
French use commas for decimal points.
- Or you could use another letter: e.g. F3, in
the E or comment columns, meaning Floor., but Americans use Floor
instead of Down.
- R for rift is likely to be confused with R for
right if put in the comment column.
- A for Alternate is the best I can think of. Obviously
you could just pick any letter, but we have been careful thoughout
to use easy-to-remember abbreviations so something completely
arbitrary is not a good idea.
| Bit of Cave
| L
| R
| U
| D
| E
| Comment
| Explanation
|
 | n
| ~n | n | n |
| | L & R are defined as the bisector of the legs. For the last station they are perpendicular to the last leg. ~ is used to indicate estimated distances (very useful to know which numbers may be suspect when drawing up)
|
 | (n)
| n | n | n |
| (220) | Where L or R in standard direction is unhelpful, irrelevant or meaningless another direction is given. The approximate bearing is given in the comments field.
|
| Pn Pn | Pn P(n) |
Pn P(n) | Pn P(n) | | (NE)(160)(260)
| For pitches give NSEW instead of LRUD.
Where NSEW is not appropriate (e.g. axes of elliptical shaft lie in another orientation) then use bracket notation to give bearings |
 | Jn
| n | n | n |
| | At a Junction the value that would otherwise disappear down the joining passage is given as where the wall would have been if the joining passage was not there.
|
 | Jn
| Jn | n | n |
n | | When a survey ends at a junction the L & R values for the surveyed passage as if it continued are given. Also given is the 'Extension'. The distance that the survey leg would need to be continued to meet the wall.
|
 | n
| n | Jn | n |
n | | At a point where a passage meets a pitch The extension is given to the far wall and the roof or floor (roof in the example) is given using the Junction notation.
|
 | C
| n | n | n |
| | For a perimeter survey use C (for Chamber) in either the L (anticlockwise survey) or R (clockwise) column. Readings are on bisectors of legs
|
 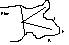 | C C Cn | C C Cn | n n n
| n n n | C n n | |
For a radial survey the centre point is given like this
Then
the other give the Extension value to the wall, as well as U & DIn more complex areas L & R values can also be given if they are significant
|
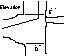 | n
| n | Jn | Jn |
Jn | | For more complicated bits of the cave the notations given can be combined to fit the need
|








